Ergodic Theory: An example
Ergodic theory is a branch of dynamical systems dealing with questions
of averages. Many simple dynamical systems are known to be chaotic,
which implies that long-term predictions are impossible from initial
data with limited accuracy. Sometimes, ergodic theory can make
predictions about the average behavior, even when systems are
chaotic.
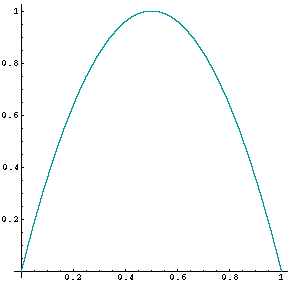 One of the simplest examples is given by iterating the map defined by
T:[0,1]->[0,1], where T(x)=4x(1-x).
This map is illustrated on the left. This map belongs to the family of Logistic maps
which in turn is part of the more general family of unimodal maps.
The Logistic maps are all of this form, except that the number 4 is replaced
by a parameter a which is allowed to vary between 1 and 4.
As a varies, the maps exhibit a large number of interesting
'bifurcations' and it has been relatively recently shown that a 'large set' of
maps in the logistic family have an invariant density (see below).
One of the simplest examples is given by iterating the map defined by
T:[0,1]->[0,1], where T(x)=4x(1-x).
This map is illustrated on the left. This map belongs to the family of Logistic maps
which in turn is part of the more general family of unimodal maps.
The Logistic maps are all of this form, except that the number 4 is replaced
by a parameter a which is allowed to vary between 1 and 4.
As a varies, the maps exhibit a large number of interesting
'bifurcations' and it has been relatively recently shown that a 'large set' of
maps in the logistic family have an invariant density (see below).
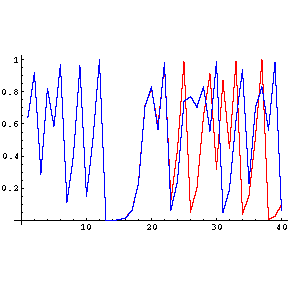 The chaotic behaviour of the map is
illustrated by the second figure which shows the orbits
Tn(x1) and
Tn(x2) for two points x1 and
x2 which differ by 10-8 and 1<=n<=40.
Note that after about 24 steps, the orbits have diverged completely. This is
typical
behavior for chaotic systems and is sometimes referred to as sensitive
dependence on initial conditions.
The chaotic behaviour of the map is
illustrated by the second figure which shows the orbits
Tn(x1) and
Tn(x2) for two points x1 and
x2 which differ by 10-8 and 1<=n<=40.
Note that after about 24 steps, the orbits have diverged completely. This is
typical
behavior for chaotic systems and is sometimes referred to as sensitive
dependence on initial conditions.
We see from this that long-term predictions are impossible in that given a
point to finite precision, we cannot calculate accurately Tn(x).
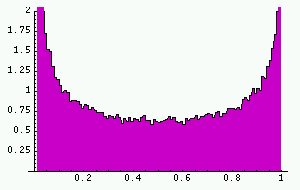 In spite of this, it is possible to make good long-term average predictions.
To produce this histogram, the interval was divided into 100 subintervals of
length 0.01, and the proportion of time that the first 100000 points on the
orbit of 0.3 spent in each subinterval was recorded. It is noticeable that
this 'density' has a relatively smooth form. It turns out to be possible to
calculate this density theoretically. It is called the 'invariant density'
and the formula for it is p(x)=pi(x(1-x))-1/2. This function is graphed below.
In spite of this, it is possible to make good long-term average predictions.
To produce this histogram, the interval was divided into 100 subintervals of
length 0.01, and the proportion of time that the first 100000 points on the
orbit of 0.3 spent in each subinterval was recorded. It is noticeable that
this 'density' has a relatively smooth form. It turns out to be possible to
calculate this density theoretically. It is called the 'invariant density'
and the formula for it is p(x)=pi(x(1-x))-1/2. This function is graphed below.
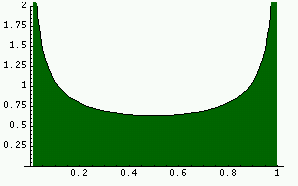 It can be shown that for almost every initial point (in the sense of
Lebesgue measure), the histogram produced by looking at the densities
of orbits in [0,1] converges to the true invariant density as the
number of points on the orbit tends to infinity and the number n
of intervals in the histogram increases to infinity.
It can be shown that for almost every initial point (in the sense of
Lebesgue measure), the histogram produced by looking at the densities
of orbits in [0,1] converges to the true invariant density as the
number of points on the orbit tends to infinity and the number n
of intervals in the histogram increases to infinity.
One important consequence of this is that if we want to calculate an
average of a function along an orbit (an important example of this is
in calculating Lyapunov exponents which measure `local stretching'),
then we may instead calculate an average over the `phase space'
([0,1]). That is for a function f, we have that for almost all x,
the average of f(Ti(x)) as i runs from 1 to n
converges to the integral of f(x)p(x) over [0,1], where p(x)
is the invariant density function described above.
This is known as Birkhoff's Pointwise Ergodic theorem and this is one of the
key results in ergodic theory. The theorem dates from 1927.
This is often described by saying that the time average and space
average are equal.
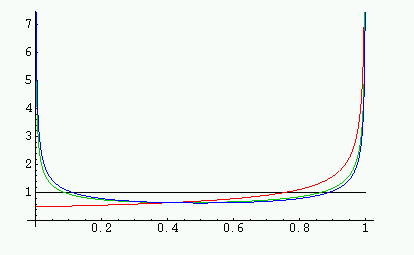 Another way of finding the invariant density is to look for fixed points
of the Ruelle-Perron-Frobenius operator. This is a linear map which allows
one to look at the evolution of a family of densities. If one starts off
with an initial distribution of measure on the interval, then applying the
map stretches out the measure and `folds it over'. The new density at a
given point x depends on the densities at the two preimages of x.
Specifically, the new density is the sum of the densities at the preimages
divided by the absolute value of the derivative of the map there.
This map from the densities to themselves was introduced by Ruelle and is
an important tool in ergodic theory. For the logistic map, if one starts off
with an initial density f0=1, and applies the operator to
get a sequence f1, f2,
f3..., they converge rapidly to the true invariant density,
p(x). In the figure f0 is plotted in black,
f1 in red, f2 in green and p(x)
in blue.
Another way of finding the invariant density is to look for fixed points
of the Ruelle-Perron-Frobenius operator. This is a linear map which allows
one to look at the evolution of a family of densities. If one starts off
with an initial distribution of measure on the interval, then applying the
map stretches out the measure and `folds it over'. The new density at a
given point x depends on the densities at the two preimages of x.
Specifically, the new density is the sum of the densities at the preimages
divided by the absolute value of the derivative of the map there.
This map from the densities to themselves was introduced by Ruelle and is
an important tool in ergodic theory. For the logistic map, if one starts off
with an initial density f0=1, and applies the operator to
get a sequence f1, f2,
f3..., they converge rapidly to the true invariant density,
p(x). In the figure f0 is plotted in black,
f1 in red, f2 in green and p(x)
in blue.
Ergodic theory has advanced considerably since that time, but there are still
a large number of accessible problems to work on and it continues to be an
active field, with applications to many other areas of mathematics, including
probability theory, information theory, differential geometry and number theory.
 One of the simplest examples is given by iterating the map defined by
T:[0,1]->[0,1], where T(x)=4x(1-x).
This map is illustrated on the left. This map belongs to the family of Logistic maps
which in turn is part of the more general family of unimodal maps.
The Logistic maps are all of this form, except that the number 4 is replaced
by a parameter a which is allowed to vary between 1 and 4.
As a varies, the maps exhibit a large number of interesting
'bifurcations' and it has been relatively recently shown that a 'large set' of
maps in the logistic family have an invariant density (see below).
One of the simplest examples is given by iterating the map defined by
T:[0,1]->[0,1], where T(x)=4x(1-x).
This map is illustrated on the left. This map belongs to the family of Logistic maps
which in turn is part of the more general family of unimodal maps.
The Logistic maps are all of this form, except that the number 4 is replaced
by a parameter a which is allowed to vary between 1 and 4.
As a varies, the maps exhibit a large number of interesting
'bifurcations' and it has been relatively recently shown that a 'large set' of
maps in the logistic family have an invariant density (see below).
 The chaotic behaviour of the map is
illustrated by the second figure which shows the orbits
Tn(x1) and
Tn(x2) for two points x1 and
x2 which differ by 10-8 and 1<=n<=40.
Note that after about 24 steps, the orbits have diverged completely. This is
typical
behavior for chaotic systems and is sometimes referred to as sensitive
dependence on initial conditions.
The chaotic behaviour of the map is
illustrated by the second figure which shows the orbits
Tn(x1) and
Tn(x2) for two points x1 and
x2 which differ by 10-8 and 1<=n<=40.
Note that after about 24 steps, the orbits have diverged completely. This is
typical
behavior for chaotic systems and is sometimes referred to as sensitive
dependence on initial conditions.
 In spite of this, it is possible to make good long-term average predictions.
To produce this histogram, the interval was divided into 100 subintervals of
length 0.01, and the proportion of time that the first 100000 points on the
orbit of 0.3 spent in each subinterval was recorded. It is noticeable that
this 'density' has a relatively smooth form. It turns out to be possible to
calculate this density theoretically. It is called the 'invariant density'
and the formula for it is p(x)=pi(x(1-x))-1/2. This function is graphed below.
In spite of this, it is possible to make good long-term average predictions.
To produce this histogram, the interval was divided into 100 subintervals of
length 0.01, and the proportion of time that the first 100000 points on the
orbit of 0.3 spent in each subinterval was recorded. It is noticeable that
this 'density' has a relatively smooth form. It turns out to be possible to
calculate this density theoretically. It is called the 'invariant density'
and the formula for it is p(x)=pi(x(1-x))-1/2. This function is graphed below.
 It can be shown that for almost every initial point (in the sense of
Lebesgue measure), the histogram produced by looking at the densities
of orbits in [0,1] converges to the true invariant density as the
number of points on the orbit tends to infinity and the number n
of intervals in the histogram increases to infinity.
It can be shown that for almost every initial point (in the sense of
Lebesgue measure), the histogram produced by looking at the densities
of orbits in [0,1] converges to the true invariant density as the
number of points on the orbit tends to infinity and the number n
of intervals in the histogram increases to infinity.
 Another way of finding the invariant density is to look for fixed points
of the Ruelle-Perron-Frobenius operator. This is a linear map which allows
one to look at the evolution of a family of densities. If one starts off
with an initial distribution of measure on the interval, then applying the
map stretches out the measure and `folds it over'. The new density at a
given point x depends on the densities at the two preimages of x.
Specifically, the new density is the sum of the densities at the preimages
divided by the absolute value of the derivative of the map there.
This map from the densities to themselves was introduced by Ruelle and is
an important tool in ergodic theory. For the logistic map, if one starts off
with an initial density f0=1, and applies the operator to
get a sequence f1, f2,
f3..., they converge rapidly to the true invariant density,
p(x). In the figure f0 is plotted in black,
f1 in red, f2 in green and p(x)
in blue.
Another way of finding the invariant density is to look for fixed points
of the Ruelle-Perron-Frobenius operator. This is a linear map which allows
one to look at the evolution of a family of densities. If one starts off
with an initial distribution of measure on the interval, then applying the
map stretches out the measure and `folds it over'. The new density at a
given point x depends on the densities at the two preimages of x.
Specifically, the new density is the sum of the densities at the preimages
divided by the absolute value of the derivative of the map there.
This map from the densities to themselves was introduced by Ruelle and is
an important tool in ergodic theory. For the logistic map, if one starts off
with an initial density f0=1, and applies the operator to
get a sequence f1, f2,
f3..., they converge rapidly to the true invariant density,
p(x). In the figure f0 is plotted in black,
f1 in red, f2 in green and p(x)
in blue.